二元函数的极值及其求法

1.求该二元函数的梯度，并令其等于零，求出所有驻点（X0，Y0）。
即解方程组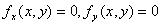
2.判别驻点是否为极值点。判别方法如下：对原函数求二阶导，并将该驻点代入求得A，B，C.并根据判别公式判断该驻点是否为极值点。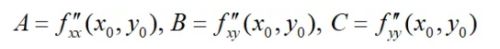

3.(1) 如果A>0，且AC-B^2>0，则f(x,y)在(x0,y0)处取极小值；
(2) 如果A<0，且AC-B^2>0，则f(x,y)在(x0,y0)处取极大值；
(3) 如果AC-B^2<0，则f(x,y)在(x0,y0)处不取极值．
4.对于有约束的多元函数极值，最值问题，通常使用拉格朗日乘数法或者代入法（降低未知参数个数）。