机器学习代码实现:线性回归与岭回归

1.线性回归模型

线性回归模型是最简单的一种线性模型，模型的形式就是：
$y=W^T x+b$
我们可以通过对原本的输入向量x扩增一个为1的维度将参数W和b统一成一个参数W，即模型变成了
$y=W^T x$
这里的W是原本两个参数合并之后的而其损失函数的形式是残差平方损失RSS
$L=\frac{1}{2 m} \sum_{i=1}^m\left(W^T x_i-y_i\right)^2=\frac{1}{2 m}\left(W^T X-y\right)^T\left(W^T X-y\right)$
我们很容易就可以通过求导得到线性回归模型的关于W的梯度
$\nabla_W L=\frac{1}{m} \sum_{i=1}^m\left(W^T x_i-y_i\right) x_i=\frac{1}{m} X^T\left(W^T X-y\right)$
这样一来我们就可以通过梯度下降的方式来训练参数W，可以用下面的公式表示
$W:=W-\alpha \frac{1}{m} X^T\left(W^T X-y\right)$
但实际上线性模型的参数W可以直接求解出，即：
$W=\left(X^T X\right)^{-1} X^T y$

2.线性回归的编程实现

具体代码中的参数的形式可能和上面的公式推导略有区别，我们实现了一个LinearRegression的类，包含fit，predict和loss三个主要的方法，fit方法就是求解线性模型的过程，这里我们直接使用了正规方程来解

class LinearRegression:
    def fit(self, X: np.ndarray, y: np.ndarray) -> float:
        N, D = X.shape
        # 将每个样本的特征增加一个维度，用1表示，使得bias和weight可以一起计算
        # 这里在输入的样本矩阵X末尾增加一列来给每个样本的特征向量增加一个维度
        # 现在X变成了N*(D+1)维的矩阵了
        expand_X = np.column_stack((X, np.ones((N, 1))))
        self.w = np.matmul(np.matmul(np.linalg.inv(np.matmul(expand_X.T, expand_X)), expand_X.T), y)
        return self.loss(X, y)

predict实际上就是将输入的矩阵X放到模型中进行计算得到对应的结果，loss给出了损失函数的计算方式：

def loss(self, X: np.ndarray, y: np.ndarray):
        """
        线性回归模型使用的是RSS损失函数
        :param X:需要预测的特征矩阵X，维度是N*D
        :param y:标签label
        :return:
        """
        delta = y - self.predict(X)
        total_loss = np.sum(delta ** 2) / X.shape[0]
        return total_loss

3.岭回归Ridge Regression与代码实现

岭回归实际上就是一种使用了正则项的线性回归模型，也就是在损失函数上加上了正则项来控制参数的规模，即：
$L=\frac{1}{2 m} \sum_{i=1}^m\left(W^T x_i-y_i\right)^2+\lambda\|W\|_2=\frac{1}{2 m}\left(W^T X-y\right)^T\left(W^T X-y\right)+\lambda W^T W$
因此最终的模型的正规方程就变成了：
$W=\left(X^T X+\lambda I\right)^{-1} X^T y$
这里的\lambda是待定的正则项参数，可以根据情况选定，岭回归模型训练的具体代码如下

class RidgeRegression:
    def fit(self, X: np.ndarray, y: np.ndarray):
        N, D = X.shape
        I = np.identity(D + 1)
        I[D][D] = 0
        expand_X = np.column_stack((X, np.ones((N, 1))))
        self.W = np.matmul(np.matmul(np.linalg.inv(np.matmul(expand_X.T, expand_X) 
                                                   + self.reg * I), expand_X.T), y)
        return self.loss(X, y)

4.数据集实验
这里使用了随机生成的二位数据点来对线性模型进行测试，测试结果如下：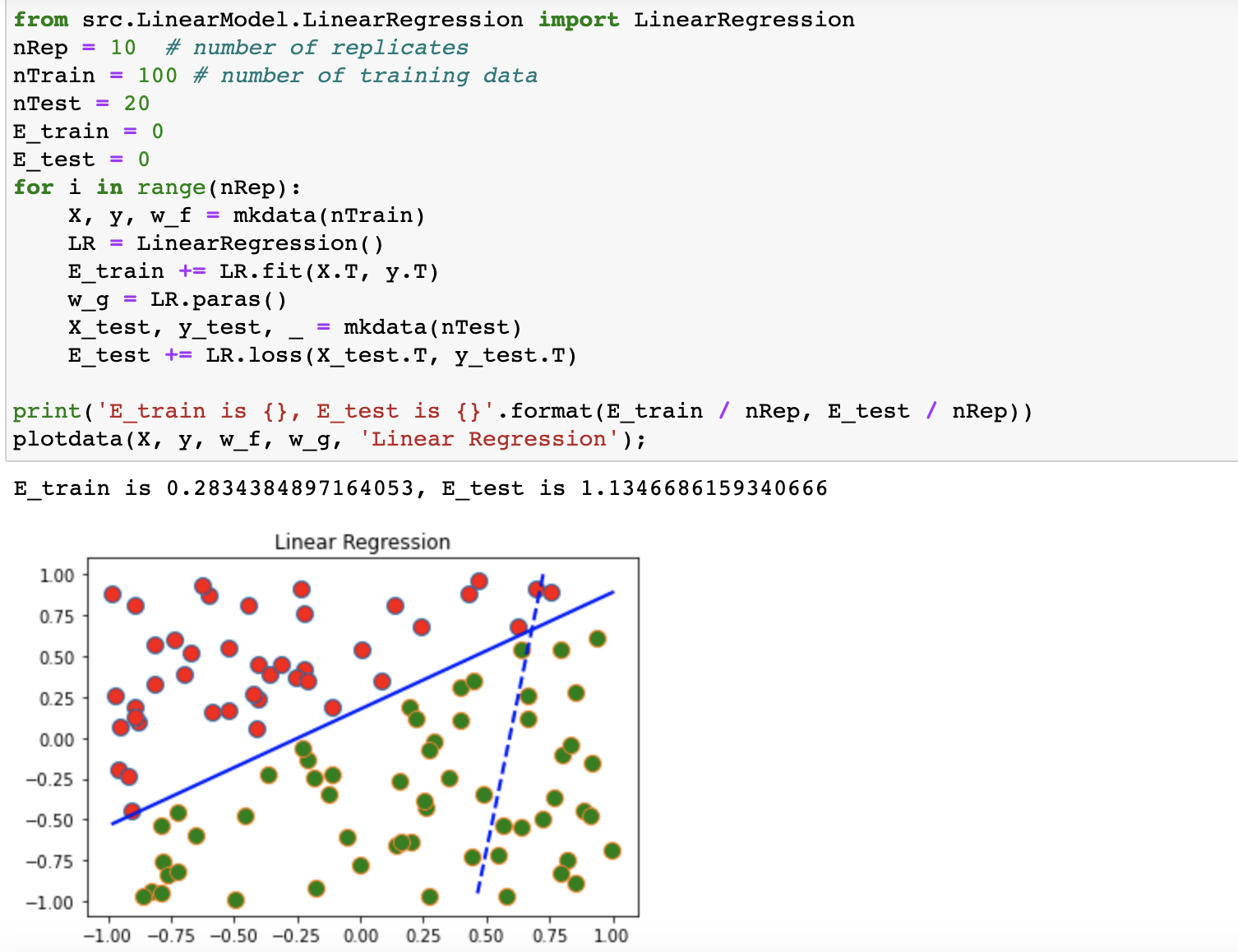

线性模型测试结果
岭回归也使用同样的代码进行测试。